Enero

Series de Laurent

Si f(z) no es analítica en Zo, entonces no admite desarrollo mediante serie de Taylor. En este caso se define la serie de Laurent que es propia de funciones de variable compleja.

sea: 

&1:| Z-Zo | > r  y  &2:| Z-Zo | < R  ;  r < R donde: D={Z€C/r<|Z-Zo|

Sea f : D©C→C, función analítica dentro y sobre la frontera de D, entonces: 

donde: an y bn son los coeficientes de la Serie de Laurent.

-Teorema:

Sea f(z) analítica en el anillo r<|Z-Zo|

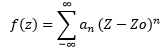
donde:

FUNCIONES PERIÓDICAS Y ORTOGONALES

DEFINICIÓN.
PROPIEDADES
EJERCICIOS

ENLACE:
https://docs.google.com/presentation/d/1WkAaZv9ylEV4A9wa8BZ0Mlsu6HW8I1Xwrf2DJuud168/edit#slide=id.p4

SERIES DE FOURIER

DEMOSTRACIÓN.
PROPIEDADES
EJERCICIOS
ENLACE: 

https://docs.google.com/presentation/d/1tSM6e8BuCP8VkER3PwQ-L6fqPJ_w1CBka9azs9qVGhs/edit#slide=id.p4

SERIES DE FOURIER de Funciones Especiales

DEMOSTRACIÓN.
EJERCICIOS
ENLACE: 

https://docs.google.com/presentation/d/1lwRBFZZESyA13iFeJ7mp61114N2VCUNSSwyfVaMvotc/edit#slide=id.p3

TRANSFORMADA DE FOURIER

PROPIEDADES
EJERCICIOS
ENLACE:
https://docs.google.com/presentation/d/16o48qZo2SE16j3KT57rDmcmfVvtV2VYr09rZHN3Y42U/edit#slide=id.p

TRANSFORMADA DE FOURIER de Funciones Especiales

RESOLUCIÓN DE EJERCICIOS
ENLACE:
https://docs.google.com/presentation/d/1XvNwn2KKrNr50OlNsR50UoYd71tVTGan5xjYkZFSN4E/edit